等离子体在PCB工艺中的各凹蚀 因素交互作用分析

0 引言
影响等离子凹蚀效果的因素有功率、气体总量、气体混合比值、凹蚀时间、温度等因素，这些因素不仅直接影响着试验结果，而且因素之间的交互作用也同样对结果产生影响，所谓交互作用指的就是某些因素间各水平的联合搭配对试验结果产生的影响，这种联合作用就称为交互作用。本文将根据凹蚀的正交试验阐述并分析等离子各因素的交互作用，分析结果可以为等离子凹蚀提供参考。
1 凹蚀实验
1.1 实验器材
等离子机（Plasma Etch—Carson City.NV—Made in USA），25 µm厚PI单面覆铜板，电子分析天平。
1.2 实验内容
为得到最佳凹蚀效果，选择等离子凹蚀试验的因素，包括功率、气体总量、气体比例、凹蚀时间，但本次试验不选择温度，原因是根据资料信息和笔者以往的试验经验，凹蚀处理对温度要求不高，因此只需要将试验温度控制在正常范围之内即可。需要说明的是，为了便于考察因素之间的交互作用，每个试验因素都选择两个试验水平，这样简单明了，而且各试验因素水平都是在对以往的实验结果和资料信息的综合分析之后才加以选择的，具有整齐可比，均匀分散的特点。因素水平的选择如表1，至于两种气体（四氟化碳和氧气）的比例是笔者以往凹蚀最佳实验效果的参数，在此仅用A1与A2表示（表1）。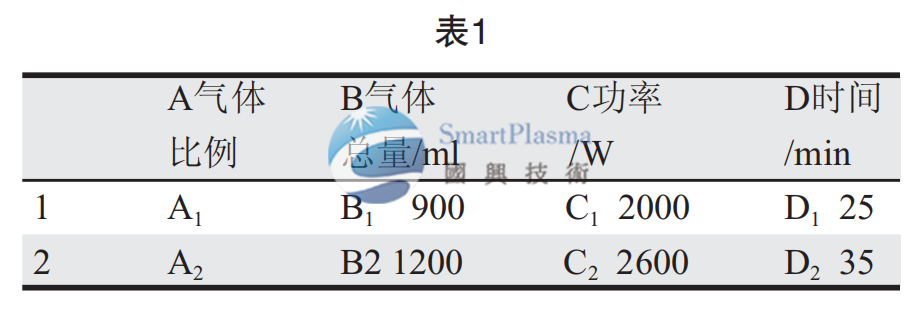

根据以往的试验结果分析，在等离子凹蚀试验中可能产生交互作用的因素有气体比例，气体总量和功率。因此选择需要考察的交互作用为：气体比例和气体总量，气体比例和功率，气体总量和功率之间的交互作用，即A×B，A×C，B×C。由于正交试验考虑到交互作用，那么在设计正交试验表时，因素和需要考察的交互作用就需要合理的安排在正交表的表头上，因此正交表的选择就尤为重要。一般来说，对于考虑交互作用的正交表的选取应该遵循一个原则，即考察因素的自由度及交互作用的自由度总和必须不大于所选正交表的总自由度。自由度的计算标准为：正交表的总自由度f总＝试验次数－1；因素自由度为f＝因素水平数－1，交互作用的自由度为两交互因素的自由度之积。在本次试验中由于每个因素只安排了两个水平，则根据上面自由度的计算准则，A，B，C，D的自由度为：fA＝fB＝fC＝fD＝2－1＝1；交互作用A× B，A×C，B×C的自由度为，fA×B＝fA×fB＝1，同理，fA×C＝fA×fC＝1，fB×C＝fB×fC＝1，由此可见本次试验中因素及交互作用的自由度总和＝fA＋fB＋fC ＋fD＋fA×B＋fA×C＋fB×C＝7，因此可以选择正交表L8 （27）安排试验，因为该正交表的总自由度为：f总＝ 8－1＝7，正好满足选择正交表所遵循的原则，故可以选择L8（27）安排试验，同时关于正交表表头设计还应遵循以下两点：
（1）首先考虑交互作用的因素A与B，将A放在第1列，将B放在第2列，再查询L8（27）交互作用表可得A×B为第3列。
（2）再考虑有交互作用的C，将C放在第4列，
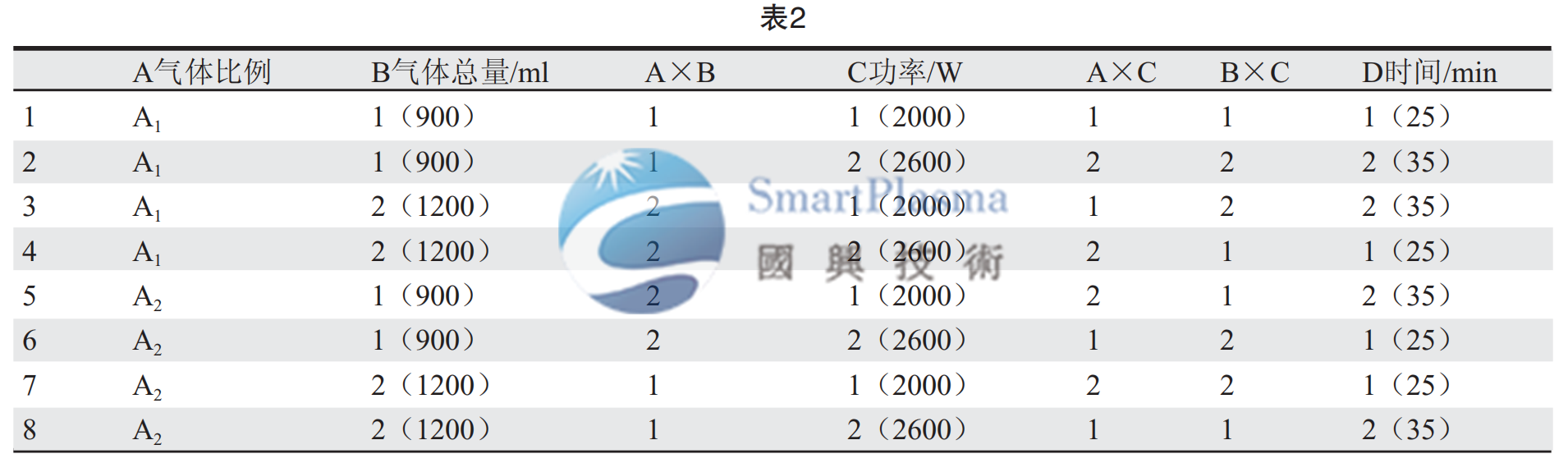
由L8（27）交互作用表可得A×C占第5列，B×C占 第6列，D排在最后一列。综合以上各原则，可设计正交表（表2）安排试
验。以表2来安排8组试验，所测试的试验结果即凹蚀量用质量差来表示，具体做法是对比单面覆铜板在试验前后的质量差（用电子天平分析测量），该质量差代表着等离子体对PI的凹蚀效果，以此为标准，做8次试验得到8组数据，为了科学分析各因素及交互作用对实验结果的影响，还要对各因素和交互作用进行极差分析，并以此判断那些因素对实验结果的影响大，那些因素对试验结果影响小，同时还可以判断对实验结果影响大的因素取那个水平将对实验结果更加有利。

1.3 实验结果分析
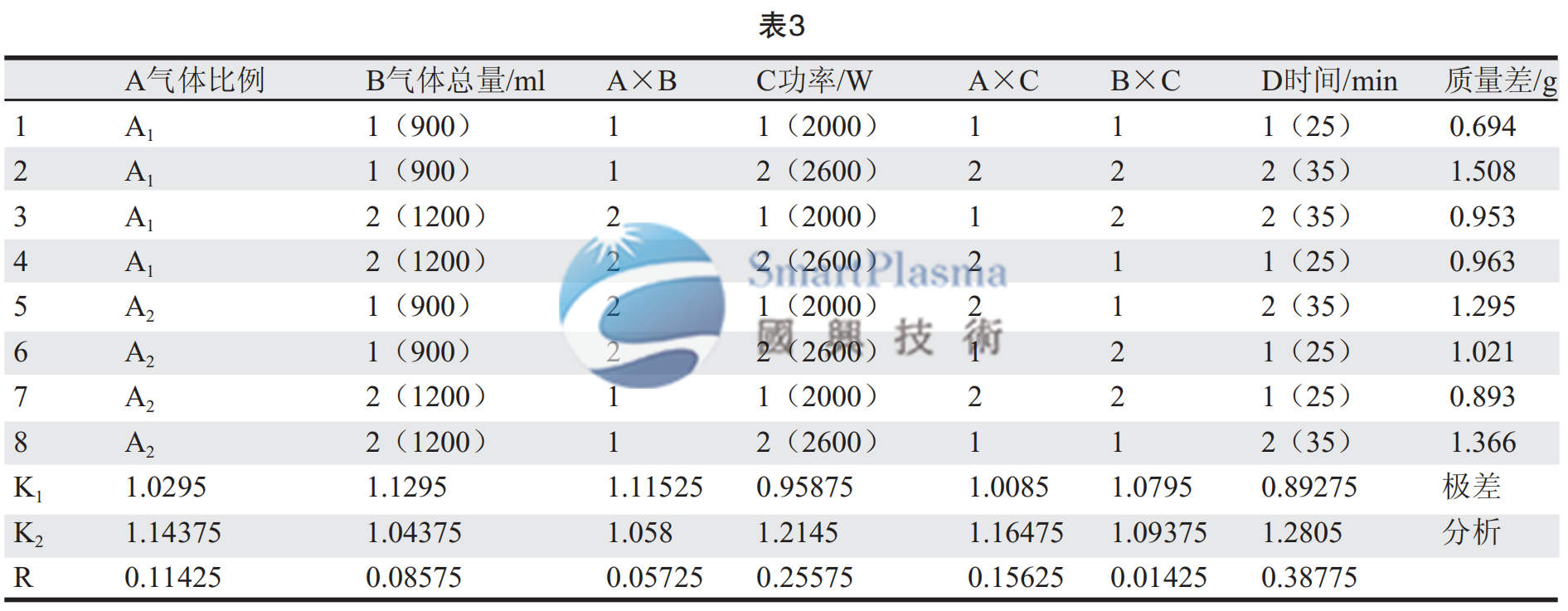
试验结果的质量差（凹蚀量）和极差分析如表3所示。现在以A因素为例，阐述极差分析的原理和计算，将A因素的两个水平所对应的试验结果分成两组，即A1和A2两组，分别取这两组试验结果的平均值：
K1＝（0.694＋1.508＋0.953＋0.963）/4＝1.0295
K2＝（1.295＋1.021＋0.893＋1.366）/4＝1.14375
然后将K1和K2中的最大值减去最小值，就得出

极差值，即：
R＝1.14375－1.0295＝0.11425
其余的数据就可以以此类推然后用极差分析得出结果。由极差分析结果可知，极差大则说明两个水平对实验结果所造成的影响差别大，即通常是重要因素，而造成极差小的因素往往是不重要因素。我们由此得出本次试验的因素主次为：
（D：时间）－（C：功率）－（A×C）－
（A：气体比例）－（A：气体比例）－（B：气体
总量）－（A×B）－（B×C）

由此可见，在本试验中因素交互作用所产生的影响还是很大的，主要的影响是A×C，其次是A× B，至于B×C影响太小可以忽略，那么在这种情况下，选取试验参数就不能单独考虑，比如时间没有交互时，就可以单独考虑为35 min，而具有交互作用的因素水平的选取则应该画出二元表和二元图进行

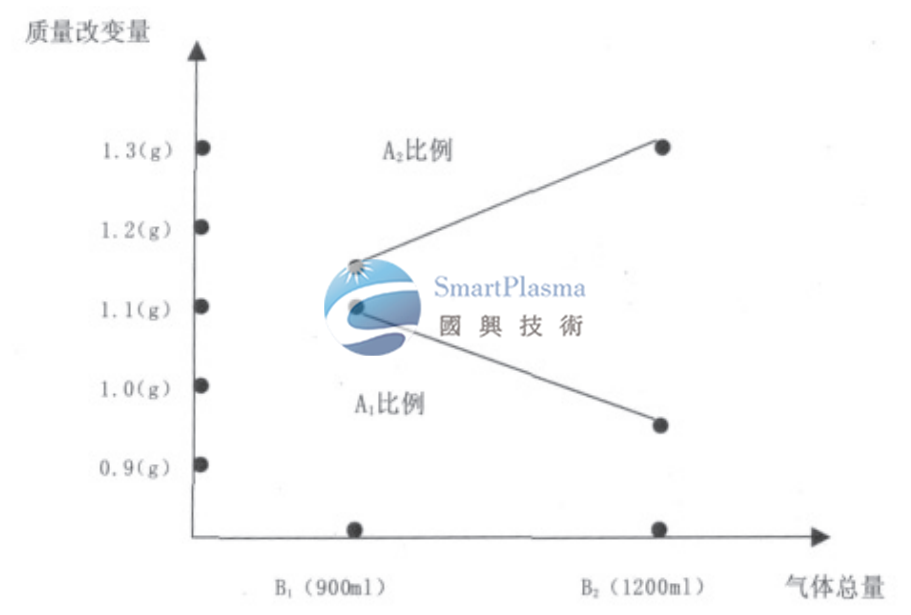
综合分析，交互作用A×C的二元表见表4，二元图见
图1所示。

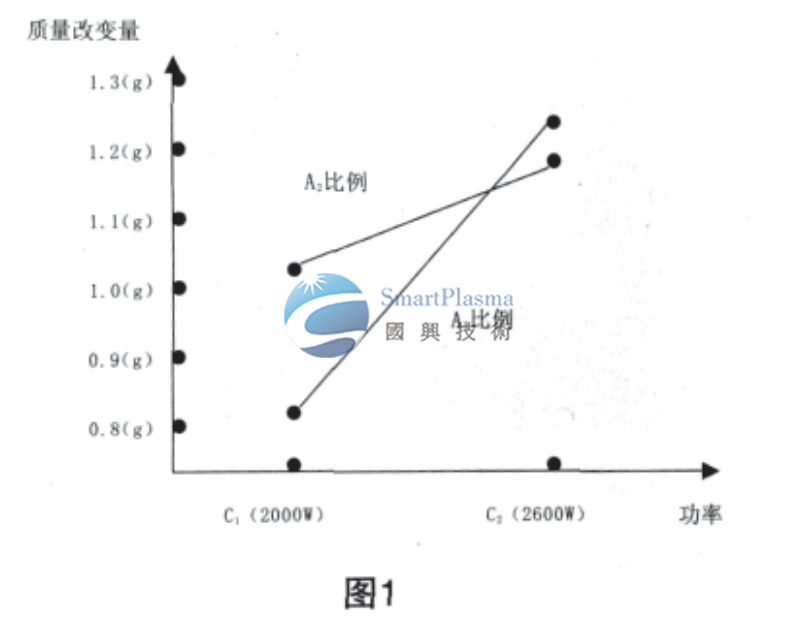
由二元表和二元图可以清晰的看出，具有交互作用因素的水平选取是需要观察他们共同作用的结果，A1C2（C2为2600 W）的搭配使得凹蚀效果最为明显。故选择A1C2。同理我们可以通过二元表（表5）和二元图（图2）确定交互作用A×B：由于A已经被前面试验所确定，即A1，所以B的确定就较为简单，在A1框中选择，应该选择B1，因为A1B1凹蚀效果最为明显。

3 实验结论
由实验结果分析可知，在等离子凹蚀试验中，各因素之间存在着交互作用，需要考虑的主要交互作用是气体比例和气体总量，气体比例和功率之间的交互作用，因此在凹蚀实践中需要充分考虑并利用这些交互作用使生产达到最优化效果。
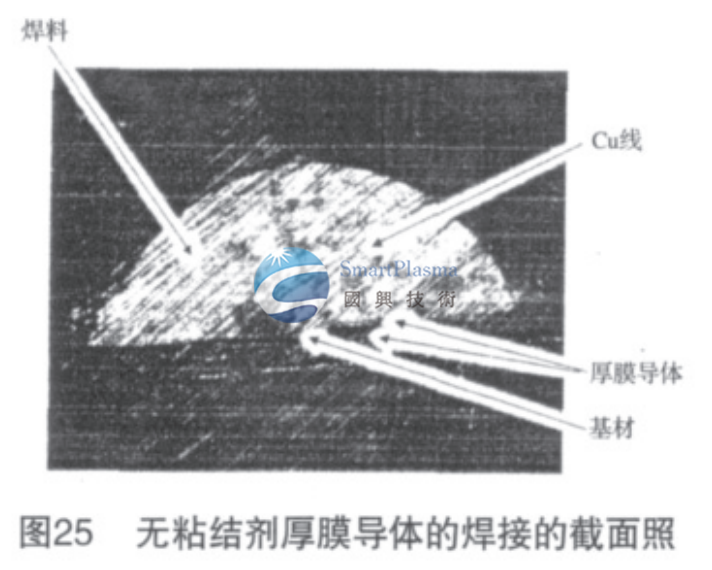
图25所示是无粘结剂厚膜电路上焊接铜线的焊盘部分的截面照片。与焊料部分相比，厚膜导体层非常薄，可以理解为厚膜导体层与焊料的亲和性良好而可以均匀接触。

4.5 纳米胶和铜胶
对于厚膜电路来说，导体用印刷胶的性能是重要的关键所在。为了提高导电率或者图形的清晰度，将导电性粒子的粒径控制在100 µm以内，即盛行开发纳米胶技术。如果评价这些纳米胶的性能，导电性和图形的清晰度确实比聚合物系厚膜电路提高了许多。然而材料成本也有相当的上升，稍有不慎就会吃掉好不容易谋求得到的低印刷工艺成本，提高了成本中的材料比率。结果适得其反，比蚀刻铜箔形成的通常PCB的成本还要高，就难以应用于消费类用电子设备上。为了代替高价的Ag导体粒子，试用了廉价的铜金属导体粒子。但是这种方法也并不完美。这是因为铜的微细粉末比Ag的稳定性差，需要进行适当的稳定性处理，这样会使成本上升，丧失与Ag导体相比较的优点。