0 引言
影響等離子凹蝕效果的因素有功率、氣體總量、氣體混合比值、凹蝕時間、溫度等因素,這些因素不僅直接影響著試驗結果,而且因素之間的交互作用也同樣對結果產生影響,所謂交互作用指的就是某些因素間各水準的聯合搭配對試驗結果產生的影響,這種聯合作用就稱為交互作用。本文將根據凹蝕的正交試驗闡述並分析等離子各因素的交互作用,分析結果可以為等離子凹蝕提供參考。
1 凹蝕實驗
1.1 實驗器材
等離子機(Plasma Etch—Carson City.NV—Made in USA),25 µm厚PI單面覆銅板,電子分析天平。
1.2 實驗內容
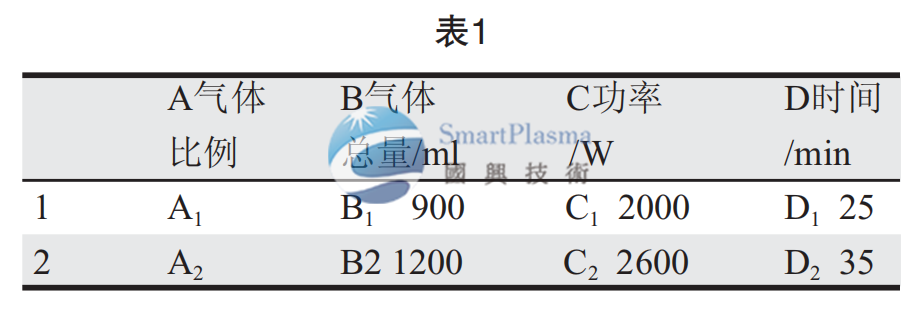
為得到最佳凹蝕效果,選擇等離子凹蝕試驗的因素,包括功率、氣體總量、氣體比例、凹蝕時間,但本次試驗不選擇溫度,原因是根據資料資訊和筆者以往的試驗經驗,凹蝕處理對溫度要求不高,因此只需要將試驗溫度控制在正常範圍之內即可。需要說明的是,為了便於考察因素之間的交互作用,每個試驗因素都選擇兩個試驗水準,這樣簡單明瞭,而且各試驗因素水準都是在對以往的實驗結果和資料資訊的綜合分析之後才加以選擇的,具有整齊可比,均勻分散的特點。因素水準的選擇如表1,至於兩種氣體(四氟化碳和氧氣)的比例是筆者以往凹蝕最佳實驗效果的參數,在此僅用A1與A2表示(表1)。
根據以往的試驗結果分析,在等離子凹蝕試驗中可能產生交互作用的因素有氣體比例,氣體總量和功率。因此選擇需要考察的交互作用為:氣體比例和氣體總量,氣體比例和功率,氣體總量和功率之間的交互作用,即A×B,A×C,B×C。由於正交試驗考慮到交互作用,那麼在設計正交試驗表時,因素和需要考察的交互作用就需要合理的安排在正交表的表頭上,因此正交表的選擇就尤為重要。一般來說,對於考慮交互作用的正交表的選取應該遵循一個原則,即考察因素的自由度及交互作用的自由度總和必須不大於所選正交表的總自由度。自由度的計算標準為:正交表的總自由度f總=試驗次數-1;因素自由度為f=因素水準數-1,交互作用的自由度為兩交互因素的自由度之積。在本次試驗中由於每個因素只安排了兩個水準,則根據上面自由度的計算準則,A,B,C,D的自由度為:fA=fB=fC=fD=2-1=1;交互作用A× B,A×C,B×C的自由度為,fA×B=fA×fB=1,同理,fA×C=fA×fC=1,fB×C=fB×fC=1,由此可見本次試驗中因素及交互作用的自由度總和=fA+fB+fC +fD+fA×B+fA×C+fB×C=7,因此可以選擇正交表L8 (27)安排試驗,因為該正交表的總自由度為:f總= 8-1=7,正好滿足選擇正交表所遵循的原則,故可以選擇L8(27)安排試驗,同時關於正交表表頭設計還應遵循以下兩點:
(1)首先考慮交互作用的因素A與B,將A放在第1列,將B放在第2列,再查詢L8(27)交互作用表可得A×B為第3列。
(2)再考慮有交互作用的C,將C放在第4列,
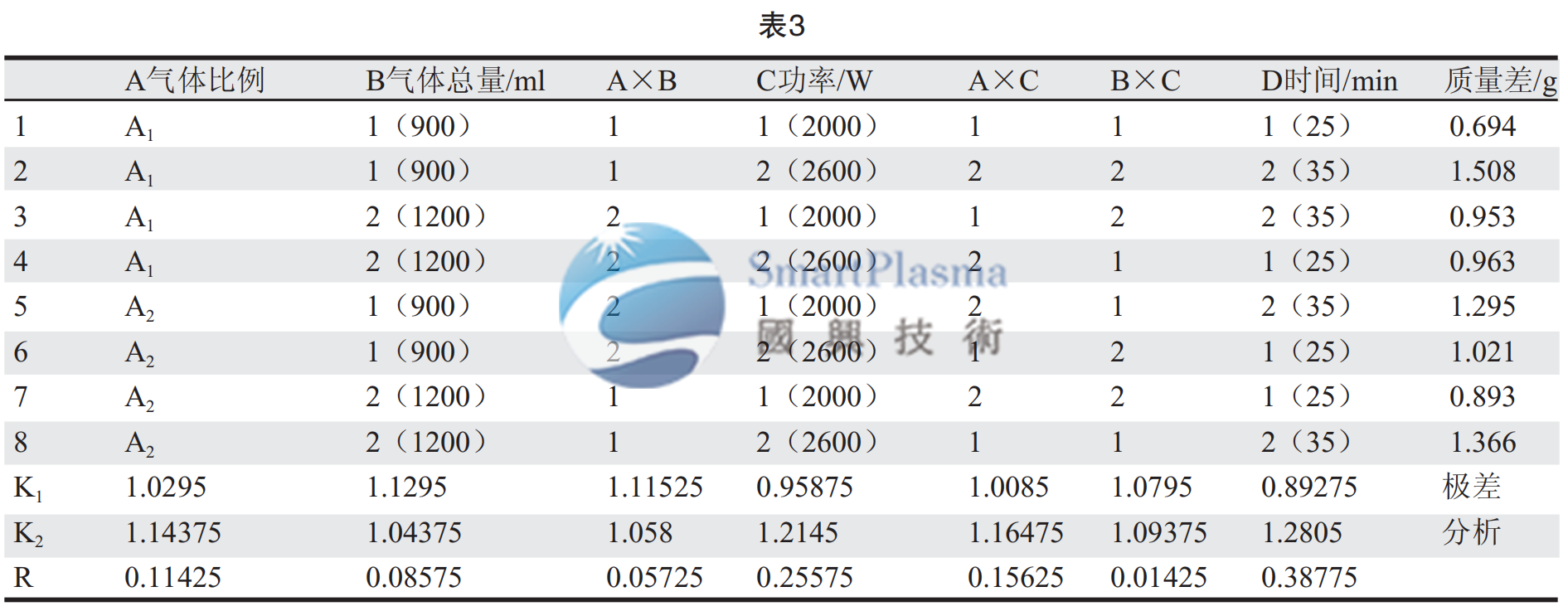
由L8(27)交互作用表可得A×C占第5列,B×C占 第6列,D排在最後一列。綜合以上各原則,可設計正交表(表2)安排試驗。以表2來安排8組試驗,所測試的試驗結果即凹蝕量用品質差來表示,具體做法是對比單面覆銅板在試驗前後的品質差(用電子天平分析測量),該品質差代表著等離子體對PI的凹蝕效果,以此為標準,做8次試驗得到8組數據,為了科學分析各因素及交互作用對實驗結果的影響,還要對各因素和交互作用進行極差分析,並以此判斷那些因素對實驗結果的影響大,那些因素對試驗結果影響小,同時還可以判斷對實驗結果影響大的因素取那個水準將對實驗結果更加有利。
1.3 實驗結果分析
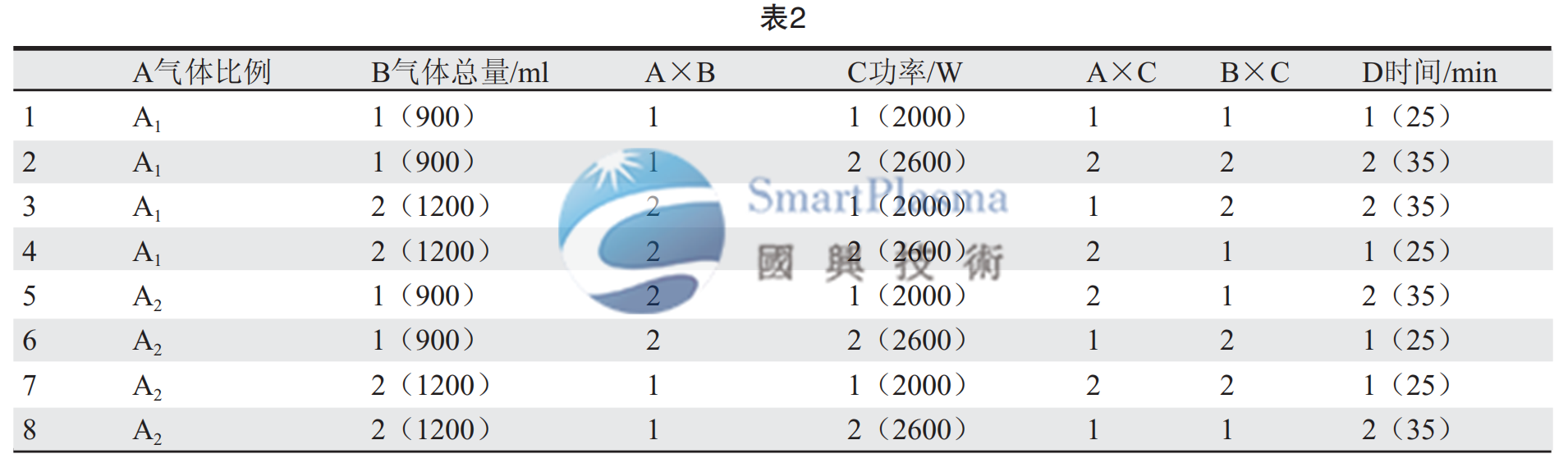
試驗結果的品質差(凹蝕量)和極差分析如表3所示。現在以A因素為例,闡述極差分析的原理和計算,將A因素的兩個水準所對應的試驗結果分成兩組,即A1和A2兩組,分別取這兩組試驗結果的平均值:
K1=(0.694+1.508+0.953+0.963)/4=1.0295
K2=(1.295+1.021+0.893+1.366)/4=1.14375
然後將K1和K2中的最大值減去最小值,就得出
極差值,即:
R=1.14375-1.0295=0.11425
其餘的數據就可以以此類推然後用極差分析得出結果。由極差分析結果可知,極差大則說明兩個水準對實驗結果所造成的影響差別大,即通常是重要因素,而造成極差小的因素往往是不重要因素。我們由此得出本次試驗的因素主次為:
(D:時間)-(C:功率)-(A×C)-
(A:氣體比例)-(A:氣體比例)-(B:氣體
總量)-(A×B)-(B×C)
由此可見,在本試驗中因素交互作用所產生的影響還是很大的,主要的影響是A×C,其次是A× B,至於B×C影響太小可以忽略,那麼在這種情況下,選取試驗參數就不能單獨考慮,比如時間沒有交互時,就可以單獨考慮為35 min,而具有交互作用的因素水準的選取則應該畫出二元表和二元圖進行
綜合分析,交互作用A×C的二元表見表4,二元圖見
圖1所示。

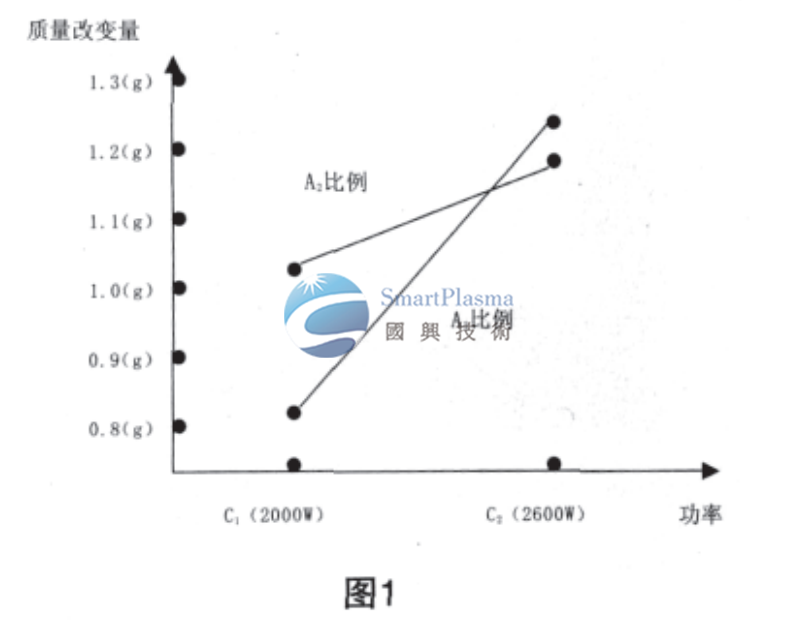
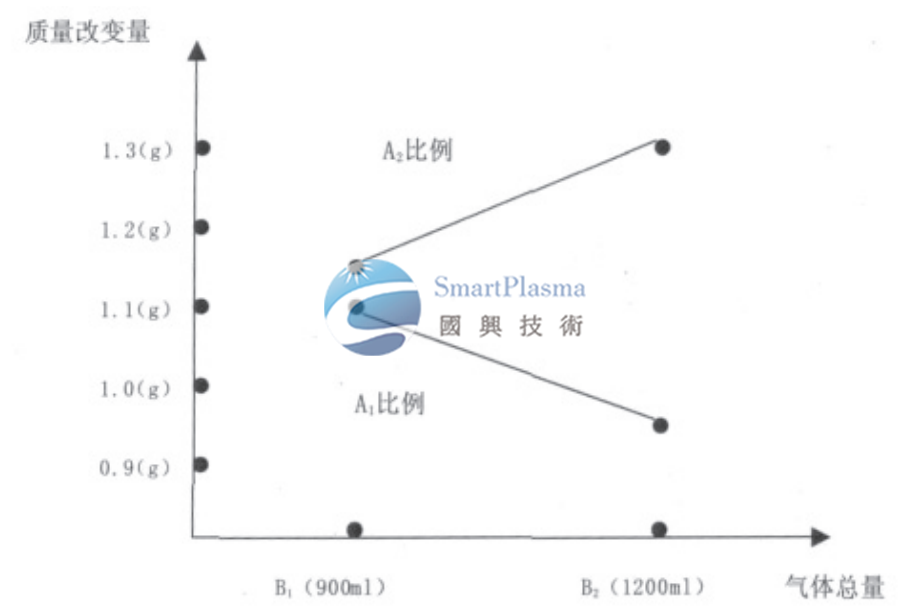
由二元表和二元圖可以清晰的看出,具有交互作用因素的水準選取是需要觀察他們共同作用的結果,A1C2(C2為2600 W)的搭配使得凹蝕效果最為明顯。故選擇A1C2。同理我們可以通過二元表(表5)和二元圖(圖2)確定交互作用A×B:由於A已經被前面試驗所確定,即A1,所以B的確定就較為簡單,在A1框中選擇,應該選擇B1,因為A1B1凹蝕效果最為明顯。

3 實驗結論
由實驗結果分析可知,在等離子凹蝕試驗中,各因素之間存在著交互作用,需要考慮的主要交互作用是氣體比例和氣體總量,氣體比例和功率之間的交互作用,因此在凹蝕實踐中需要充分考慮並利用這些交互作用使生產達到最優化效果。
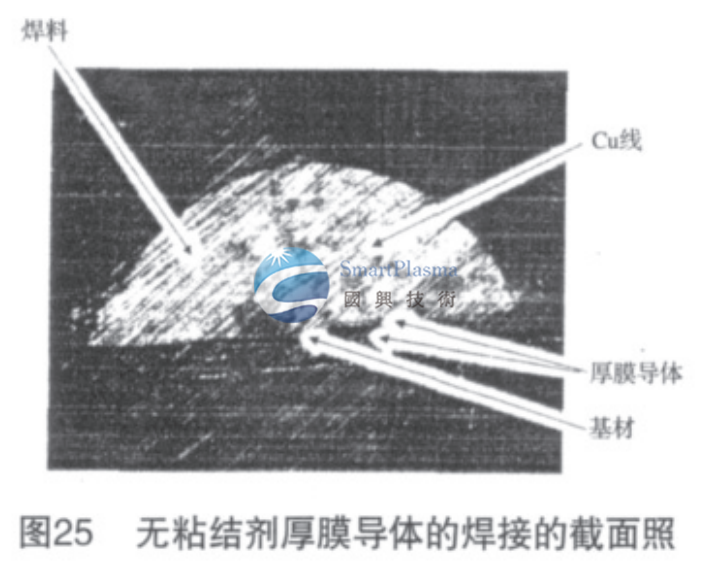
圖25所示是無粘結劑厚膜電路上焊接銅線的焊盤部分的截面照片。與焊料部分相比,厚膜導體層非常薄,可以理解為厚膜導體層與焊料的親和性良好而可以均勻接觸。
4.5 納米膠和銅膠
對於厚膜電路來說,導體用印刷膠的性能是重要的關鍵所在。為了提高導電率或者圖形的清晰度,將導電性粒子的粒徑控制在100 µm以內,即盛行開發納米膠技術。如果評價這些納米膠的性能,導電性和圖形的清晰度確實比聚合物系厚膜電路提高了許多。然而材料成本也有相當的上升,稍有不慎就會吃掉好不容易謀求得到的低印刷工藝成本,提高了成本中的材料比率。結果適得其反,比蝕刻銅箔形成的通常PCB的成本還要高,就難以應用於消費類用電子設備上。為了代替高價的Ag導體粒子,試用了廉價的銅金屬導體粒子。但是這種方法也並不完美。這是因為銅的微細粉末比Ag的穩定性差,需要進行適當的穩定性處理,這樣會使成本上升,喪失與Ag導體相比較的優點。